Honeycomb Triangles 1

 

Blaise Pascal was another famous mathematician who in 1653 published his work on a special triangle following a specific pattern.  This became known as Pascal’s triangle, even though many other cultures have studied this pattern thousands of years before.  The observations made from Pascal’s triangle has led to patterns related to probability and statistics, which we will explore later in the semester.

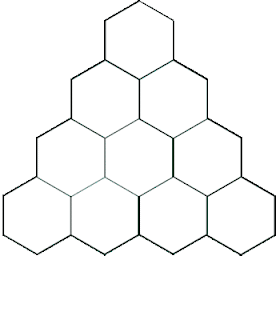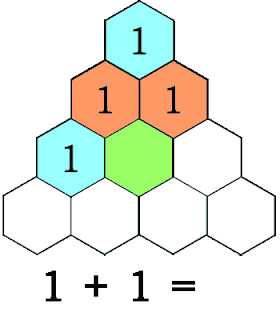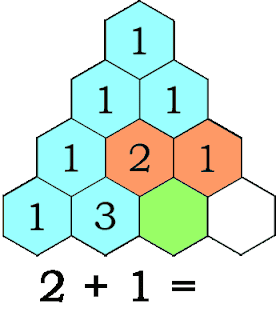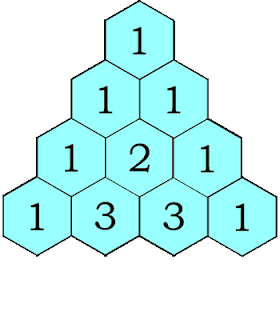
Take a look at Pascal’s triangle.  The first number starts with a 1. Then continue to place the number 1 on the left and right edge of each number 1 from above.  To obtain the missing number below, you add the two adjacent numbers above them. For example, you add the adjacent numbers 1 and 2 to obtain 3 below them.  Fill in the rest of the triangle.

 

1. Write down a few observations and patterns.  Share your observations with your group. Try to get as many observations as you can.
   
2. What happens if you color in all the odd numbers and even numbers.  What do you notice?
3. Describe where you can find these sets of numbers found in Pascal’s triangle.  Some are very easy to pick out, others may be identified by adding some of the cells together in a specific pattern.
   1. Natural numbers
   2. Fibonacci numbers
   3. Multiples of 2
   4. Multiples of 3
   5. Powers of 2: 2, 3, 8, 16
   6. Triangular numbers
   7. Square numbers
   8. Hexagonal numbers
   9. Hockey stick pattern
   10. Other patterns?

 

Resource:Mary Ann Esteban