What comes next?

  

JPN 2-1 GER

 

Desmos link

How many watermelons?

 

Can you solve it in 5 seconds?

Plant Puzzle

 

from SKG

Some solutions

Vertices Problem

from Rob Southern

 

System of Equations Puzzle

from: Matematik Dünyası

 

Runner's Puzzle

The source of this problem is

Puzzle a Day

@PuzzleADayBlog

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Exponent cartoon

Galton Board

Federer's stats

                                                          Photo by Zoë Reeve on Unsplash

source: Amy Lundy, fivethirtyeight

 

Two Numbers

Tax Collector Game

photo by Kelly Sikkema

Source of this activity:By Gary Antonick, New York Times

Tax Collector is played like this: Start with a collection of paychecks, from $1 to $12. You can choose any paycheck to keep. Once you choose, the tax collector gets all paychecks remaining that are factors of the number you chose. The tax collector must receive payment after every move. If you have no moves that give the tax collector a paycheck, then the game is over and the tax collector gets all the remaining paychecks. 

The goal is to beat the tax collector.

Example:
Turn 1: Take $8. The tax collector gets $1, $2 and $4.
Turn 2: Take $12. The tax collector gets $3 and $6 (the other factors have already been taken).

Turn 3: Take $10. The tax collector gets $5.

You have no more legal moves, so the game is over, and the tax collector gets $7, $9 and $11, the remaining paychecks. 

Total Scores:
You: $8 + $12 + $10 = $30.
Tax Collector: $1 + $2 + $3 + $4 + $5 + $6 + $7 + $9 + $11 = $48. 

Questions:

Is it possible to beat the tax collector in this $12 game? If so, how? What is the maximum score you can get?

Bonus: What if you played the game with paychecks from $1 to $24? How about $1 to $48?

 

Lockers and Bulbs

Task 1 (Source: Illustrative Math)

The 20 students in Mr. Wolf's 4th grade class are playing a game in a hallway that is lined with 20 lockers in a row.

• The first student starts with the first locker and goes down the hallway and opens all the lockers.
• The second student starts with the second locker and goes down the hallway and shuts every other locker.
• The third student stops at every third locker and opens the locker if it is closed or closes the locker if it is open.
• The fourth student stops at every fourth locker and opens the locker if it is closed or closes the locker if it is open.

This process continues until all 20 students in the class have passed through the hallway.

1. Which lockers are still open at the end of the game? Explain your reasoning.
2. Which lockers were touched by only two students? Explain your reasoning.
3. Which lockers were touched by only three students? Explain your reasoning.
4. Which lockers were touched the most? 

Make 10 Puzzles

 

 

 

 

 

 

 

 

 

  

 

 

 

 

 

 

Source: @Make_to10

 

Math Taboo Game

 

 

[download the cards from here]

Interesting root problem

 

 

circle problem

 

How to solve #area? | intersecting chord #geometry #mathriddles #maths #puzzle #shorts #Twitter pic.twitter.com/r9zvUmfrk0

— Math Lover (@GeometryPuzzles) June 20, 2022

Functions in your hand

 

Area Puzzle

 

 

Union vs Intersection Sets

 

source link

Bad Logic

 

 

A Different Perspective

 

 

The Most Common Last Digit of Multiplications

 

Source: Puzzle A Day

Two Rational Numbers

 

Source:@blatherwick_sam

Three of the many possible solutions:

Single Piece of Rope??

 

Mathematics, geometry, perception.

Using your eyes only, is it possible to determine which one consists of a single piece of rope that has its ends joined?

(Or is the task too stressful for your visual system?) pic.twitter.com/s9XkaVNCqz

— Cliff Pickover (@pickover) June 29, 2022

 

In the Shoe

 

 

What time is it?

 

Estimating and Rounding

 

 

Circle Area

 

source: @Math26039335 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Answer: 2/3

 

Distribution of World's GDP Over the Years

 

Resource and more info at: Visual Capitalist

Twelve Dots

 

 

Source:@JustinAion

Google Drive

Pythagoreas' Dream

 

  

The total area of white squares around the right-angled triangle is 450 square meters. 

Find the area of the triangle. 

altered from nRich

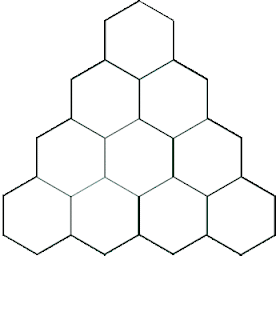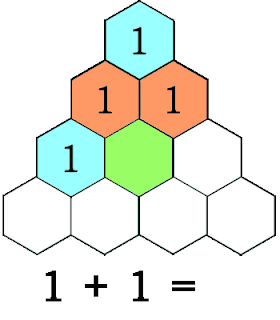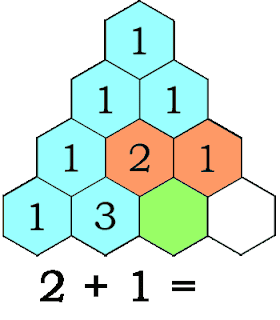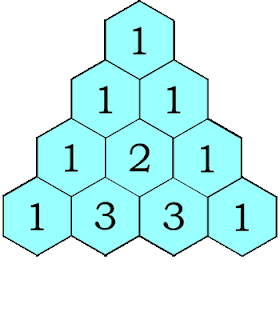
Honeycomb Triangles 2 (Hosoya's Triangle)

 

1. What patterns do you see in the above system?
2. Complete the missing hexagons. (until the row with 144, 89, ...)
3. What other patterns can you identify?

 

 

 

Honeycomb Triangles 1

 

Blaise Pascal was another famous mathematician who in 1653 published his work on a special triangle following a specific pattern.  This became known as Pascal’s triangle, even though many other cultures have studied this pattern thousands of years before.  The observations made from Pascal’s triangle has led to patterns related to probability and statistics, which we will explore later in the semester.

Take a look at Pascal’s triangle.  The first number starts with a 1. Then continue to place the number 1 on the left and right edge of each number 1 from above.  To obtain the missing number below, you add the two adjacent numbers above them. For example, you add the adjacent numbers 1 and 2 to obtain 3 below them.  Fill in the rest of the triangle.

 

1. Write down a few observations and patterns.  Share your observations with your group. Try to get as many observations as you can.
   
2. What happens if you color in all the odd numbers and even numbers.  What do you notice?
3. Describe where you can find these sets of numbers found in Pascal’s triangle.  Some are very easy to pick out, others may be identified by adding some of the cells together in a specific pattern.
   1. Natural numbers
   2. Fibonacci numbers
   3. Multiples of 2
   4. Multiples of 3
   5. Powers of 2: 2, 3, 8, 16
   6. Triangular numbers
   7. Square numbers
   8. Hexagonal numbers
   9. Hockey stick pattern
   10. Other patterns?

 

Resource:Mary Ann Esteban