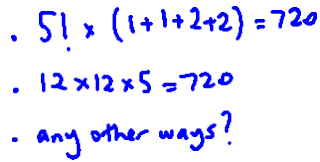What comes next?

Logic Puzzle

What replaces the question mark in the above logic puzzle?

Killer Rainbow Sudoku

Can you solve this colored sudoku without using numbers?

518

135

How Many Different Routes?

What comes next?

 

Draw a snake!

 

The following grid will be filled with numbers 1 to 64. Place the numbers in such a way that the consecutive numbers form a snake where the grid with number 1 is the head of the snake and the grid with 64 is the tail. 

You can move to the left or right, up or down but not diagonal.

 

Angles on Clock

 

Crossing the River

 

Volume Change and Similarity

Calculating the Height of Yokohama Landmark Tower

Can you find more than one way?
























Clues:

Adding Odds

Using positive odd integers and addition operation only, in how many different ways can you get 10?

Problem 153: Power Equation Puzzle

 

Problem 152: No Overlapping route

Start from the star and draw through the blue squares and come back to the star:

1. You must pass through all the blue squares and one time the most.

2. You cannot pass through the dark squares.

3. The line cannot pass through itself. 

Rich Tasks 78: Powers of 2. What do you see? What Do you wonder?

Examine the given grid above.
What patterns can you find? Try to use exponent laws. (Hint: Check diagonals)

Problem 151: Magic Squares 4

Place the numbers 1 to 36 in the above squares so that each row, column, and diagonal have the same sum: 111. Some numbers are given to help you. 

Problem 150: Magic Squares 3

Place the numbers 1 to 25 in the above squares so that each row, column, and diagonal have the same sum. Some numbers are placed to help you.

Problem 149: Magic Squares 2

Place the numbers 1 to 16 in the above squares so that each row, column, and diagonal have the same sum.

Problem 148: Magic Squares 1

Place the numbers 1 to 9 in the above squares so that each row, column, and diagonal have the same sum.

Problem 147: Sine and Cosine Rules Practice

resource: Don Steward

Rich Tasks 77: 1 billion seconds old!

How old would you be when you are 1 billion seconds old?

How many seconds would you have lived if you lived up to 100 years of age?

Problem 146: Making 720

 

Rich Tasks 77: Triangles that have their perimeters and areas equal

further info here

Rich Tasks 76: Student-Led Activity for Intersecting Chord Theorem

Problem 145: What comes next?

---

Problem 144: Three Moves

Move matches so that each pile holds 8 matches. You may add to any pile only as many matches as it already contains, and all the matches must come from one other pile. For example, if a pile holds 6 matches, you may add 6 to it, no more or less. You have three moves.



Source: Moscow Puzzles, Boris A. Kordemsky

Problem 143: Make up to 100

Problem 142: How many triangles?

Problem 141: Factorials and Exponents

Resource and inspiration from : Michael Penn

Problem 140: Power Challenge

Source: @aap03102

Problem 139: Netflix and Apple

Source