Problem 49: Mr. Oswald's phone

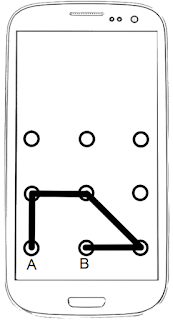
Mr. Oswald forgot the pass lock pattern on his mobile phone. He remembers that the pattern starts from the dot labeled A, and ends on the dot that is labeled B. The pattern is made by 4 strikes.

He decides to unlock his phone by trying some patterns. However after 5 wrong patterns the phone will be disabled for 5 minutes.

i.          How many different pattern can be drawn from A to B with 4 strikes?

ii.          What is the probability that he can unlock his phone without disabling it?

A pattern example is drawn on the phone image above.

Problem 48: 6-Digit Divisibility Challenge

Math Poster: Linear Equations

This week, I created 3 posters to use in my classroom.

1. Parallel lines have the same gradient. Collinear points are on the same line.

2. Equation of a Line

3. Gradient Types of Lines

PDF Versions for downloading:
Parallel Lines-Collinear Points
Equation of a Line [y-intercept form]
Gradient Types of Lines

Problem 47: Greatest Number

Problem 46: Feet and Tails

Mrs. Eleanor Abernathy has 7 female cats. This May all her cats gave birth to new kittens. Some of the cats had 3 babies, some had 4 and the remaining ones had 5 baby cats. 

The number of cats that gave birth to 5 babies is 1 less than the number of cats that have quadruplets or triplets.

Mrs. Abernathy is interested in counting and she counts 150 legs in her house. 

Can you find the number of cats who has quints(5 babies)?

Rich Tasks 11: Making Sequence Competition

Rules and Explanations
-Students can change the order of the numbers to make sequences,
-When there is a team challenge, I give the points to the first two teams who produce a sequence with a reasonable description.
-Using two dice may be better in order to emphasize term to term rule or the nth rule.

Here is another version as a worksheet.

Problem 45: Escalator Ride

 

Source 

Rich Tasks 10: Finding the Number between the Fractions

Problem 44: Hexagonal Coins

This puzzle is from one of my favorite authors, Alex Bellos. The aim is to get all 6 coins to the hexagonal order given above starting with the given order below in three moves:

You can slide any coin as long as it touches to other coins in the new position.
See the Numberphile video for details and solutions.

Problem 43: Alien Encounter

I saw this problem on another blog page. It is from Steven Strogatz's famous book Professor Stewart's Cabinet of Mathematical Curiosities. I like such Knights and Knaves type of logical reasoning questions. I use them a lot while teaching "Logic" in IB DP Math Studies course.

Here is the question:

 

---------------------

Solutions to such questions need seeing the big picture of the case, and often students struggle doing this. That's why I prefer them drawing diagrams or truth table-like charts. 

Sometimes a tree diagram from probability unit is helpful.
So let's try a solution using tree diagrams.

Assume that Alfy tells the truth. Therefore he must be a Veracitor. What he tells about Betty is also true. So Betty is Gibberish. Betty says Alfy and Gemma are same species but she is lying. Therefore Gemma must be Gibberish. This coincides with Gemma saying Betty is Veracitor, which she is not. So Gemma is a liar and it matches with what we found from Alfy and Betty's answers. So our answer is Alfy: Veracitor; Betty and Gemma: Gibberish.

It is better to see the other option where Alfy is dishonest. This time we see that, if he is a liar, then Betty must be a Veracitor. If Betty is Veracitor, then Gemma must be Gibberish since Betty is honest in this option. However being a Gibberish, Gemma must be a liar. However, Gemma says Betty to be a Veracitor which is true. This truth creates a contradiction. Therefore this option is not reasonable at all and Alfy must be telling the truth. So the answer is the previous one.

Problem 42: Pink Triangle

Although an easy one, @solvemymaths's following similarity question on Twitter went viral on the Internet, so I have decided to keep it here:

What fraction is shaded?

Problem 41: Estimation

Math Pics 4: Pentagonal Totals

I saw this on Twitter. It is an amazing work. The total of numbers on each side of the pentagon is equal to each other.

Problem 40: Patterns with Watermelons

How many watermelons will there be in the 73rd step?

Source: Visual Patterns